Elektronický vzdelávací materiál

Uhol dvoch priamok v rovine

Uhol priamok definujeme takto:

Uhol dvoch rovnobežných priamok je nulový.
Uhol dvoch rôznobežných priamok je najmenší z uhlov, ktoré priamky určujú.
Veľkosť uhla priamok p, q budeme počítať pomocou ich smerových vektorov s_p, s_q.

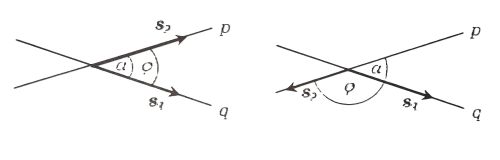
Označíme veľkosť uhla priamok a a veľkosť uhla ich smerových vektorov . Z obrázka vidieť, že môžu nastať dve situácie:

ak α = φ tak cos alpha = cos φ

ak α = π - φ tak cos α = - cos φ

V oboch prípadoch cos α = cos φ preto pre veľkosť uhla dvoch priamok p, q platí:

cos α =
|s_p * s_q|/|s_p||s_q|

Veľkosť uhla priamok p, q môžeme počítať aj pomocou ich normálových vektorov.

cos α =
|n_p * n_q|/|n_p||n_q|